Mathematics in medieval Islam
In the history of mathematics, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and developed under the Islamic civilization between circa 622 and 1600.[1] Islamic science and mathematics flourished under the Islamic caliphate established across the Middle East, extending from the Iberian Peninsula in the west to the Indus in the east and to the Almoravid Dynasty and Mali Empire in the south.
Katz, in A History of Mathematics says that:[2]
"A complete history of mathematics of medieval Islam cannot yet be written, since so many of these Arabic manuscripts lie unstudied... Still, the general outline... is known. In particular, Islamic mathematicians fully developed the decimal place-value number system to include decimal fractions, systematised the study of algebra and began to consider the relationship between algebra and geometry, studied and made advances on the major Greek geometrical treatises of Euclid, Archimedes, and Apollonius, and made significant improvements in plane and spherical geometry."
An important role was played by the translation and study of Greek mathematics, which was the principal route of transmission of these texts to Western Europe. Smith notes that:[3]
"the world owes a great debt to Arab scholars for preserving and transmitting to posterity the classics of Greek mathematics... their work was chiefly that of transmission, although they developed considerable ingenuity in algebra and showed some genius in their work in trigonometry."
Adolph P. Yushkevich states regarding the role of Islamic mathematics:[4]
The Islamic mathematicians exercised a prolific influence on the development of science in Europe, enriched as much by their own discoveries as those they had inherited by the Greeks, the Indians, the Syrians, the Babylonians,etc.
Contents |
History
Algebra
The most important contribution of the Islamic mathematicians was the development of algebra; combining Indian and Babylonian material with the Greek geometry to develop algebra.
Irrational numbers
The Greeks had discovered Irrational numbers, but were not happy with them and only able to cope by drawing a distinction between magnitude and number. In the Greek view, magnitudes varied continuously and could be used for entities such as line segments, whereas numbers were discrete. Hence, irrationals could only be handled geometrically; and indeed Greek mathematics was mainly geometrical. Islamic mathematicians including Abū Kāmil Shujāʿ ibn Aslam slowly removed the distinction between magnitude and number, allowing irrational quantities to appear as coefficients in equations and to be solutions of algebraic equations. They worked freely with irrationals as objects, but they did not examine closely their nature.[7]
Induction
The earliest implicit traces of mathematical induction can be found in Euclid's proof that the number of primes is infinite (c. 300 BCE). The first explicit formulation of the principle of induction was given by Pascal in his Traité du triangle arithmétique (1665).
In between, implicit proof by induction for arithmetic sequences was introduced by al-Karaji (c. 1000) and continued by al-Samaw'al, who used it for special cases of the binomial theorem and properties of Pascal's triangle.
Major figures and developments
Omar Khayyám
Omar Khayyám (c. 1038/48–1123/24)[8] wrote the Treatise on Demonstration of Problems of Algebra containing the systematic solution of third-degree equations, going beyond the Algebra of al-Khwārizmī.[9] Khayyám obtained the solutions of these equations by finding the intersection points of two conic sections. This method had been used by the Greeks,[10] but they did not generalize the method to cover all equations with positive roots.[11]
Sharaf al-Dīn al-Ṭūsī
Sharaf al-Dīn al-Ṭūsī (? in Tus, Iran – 1213/4) developed a novel approach to the investigation of cubic equations—an approach which entailed finding the point at which a cubic polynomial obtains its maximum value. For example, to solve the equation 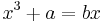 , with a and b positive, he would note that the maximum point of the curve
, with a and b positive, he would note that the maximum point of the curve 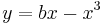 occurs at
occurs at 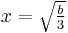 , and that the equation would have no solutions, one solution or two solutions, depending on whether the height of the curve at that point was less than, equal to, or greater than
, and that the equation would have no solutions, one solution or two solutions, depending on whether the height of the curve at that point was less than, equal to, or greater than  . His surviving works give no indication of how he discovered his formulae for the maxima of these curves. Various conjectures have been proposed to account for his discovery of them.[12]
. His surviving works give no indication of how he discovered his formulae for the maxima of these curves. Various conjectures have been proposed to account for his discovery of them.[12]
Other major figures
- Muhammad ibn Mūsā al-Khwārizmī (c. 780 – c. 850)
- 'Abd al-Hamīd ibn Turk (fl. 830) (quadratics)
- Thabit ibn Qurra (826–901)
- Abū Kāmil Shujā ibn Aslam (c. 850 – 930) (irrationals)
- Abū Sahl al-Qūhī (c. 940–1000) (centers of gravity)
- Abu'l-Hasan al-Uqlidisi (952 – 953) (arithmetic)
- 'Abd al-'Aziz al-Qabisi
- Abū al-Wafā' Būzjānī (940 – 998) (spherical trigonometry)
- Al-Karaji (c. 953 – c. 1029) (algebra, induction)
- Abu Nasr Mansur (c. 960 – 1036) (spherical trigonometry)
- Ibn Tahir al-Baghdadi (c. 980–1037) (irrationals)
- Ibn al-Haytham (ca. 965–1040)
- Abū al-Rayḥān al-Bīrūnī (973 – 1048) (trigonometry)
- Al-Khayyam (1048–1131) (cubic equations, parallel postulate)
- Ibn Yaḥyā al-Maghribī al-Samawʾal (c. 1130 – c. 1180)
- Sharaf al-Dīn al-Ṭūsī (c. 1150–1215) (cubics)
- Naṣīr al-Dīn al-Ṭūsī (1201–1274) (parallel postulate)
- Jamshīd al-Kāshī (c. 1380–1429) (decimals)
See also
- Timeline of Islamic science and technology
- Islamic Golden Age
- Hindu and Buddhist contribution to science in medieval Islam
Notes
- ^ Hogendijk 1999.
- ^ Katz 1993.
- ^ Smith 1958, Vol. 1, Chapter VII.4.
- ^ Sertima, Ivan Van (1992). Golden age of the Moor, Volume 11. Transaction Publishers. p. 394. ISBN 1560005815.
- ^ O'Connor, John J.; Robertson, Edmund F., "Al-Biruni", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Al-Biruni.html.
- ^ Douglas, A. V. (1973). "R.A.S.C. Papers- Al-Biruni, Persian Scholar". Journal of the Royal Astronomical Society of Canada 67: 973–1048. http://adsabs.harvard.edu/full/1973JRASC..67..209D.
- ^ http://www.math.tamu.edu/~dallen/history/infinity.pdf
- ^ Struik 1987, p. 96.
- ^ Boyer 1991, pp. 241–242.
- ^ Struik 1987, p. 97.
- ^ Boyer 19991, pp. 241–242.
- ^ Berggren, J. Lennart (1990). "Innovation and Tradition in Sharaf al-Dīn al-Ṭūsī's al-Muʿādalāt". Journal of the American Oriental Society 110 (2): 304–309. JSTOR 604533.
References
- Boyer, Carl B. (1991). "Greek Trigonometry and Mensuration, and The Arabic Hegemony". A History of Mathematics (2nd ed.). New York City: John Wiley & Sons. ISBN 0471543977.
- Katz, Victor J. (1993). A History of Mathematics: An Introduction. HarperCollins college publishers. ISBN 0-673-38039-4..
- Ronan, Colin A. (1983). The Cambridge Illustrated History of the World's Science. Cambridge University Press. ISBN 0521258448.
- Smith, David E. (1958). History of Mathematics. Dover Publications. ISBN 0-486-20429-4.
- Struik, Dirk J. (1987). A Concise History of Mathematics (4th rev. ed.). Dover Publications. ISBN 0486602559.
Further reading
- Books on Islamic mathematics
- Berggren, J. Lennart (1986), Episodes in the Mathematics of Medieval Islam, New York: Springer-Verlag, ISBN 0-387-96318-9
- Review: Toomer, Gerald J.; Berggren, J. L. (1988), "Episodes in the Mathematics of Medieval Islam", American Mathematical Monthly (Mathematical Association of America) 95 (6): 567, doi:10.2307/2322777, JSTOR 2322777
- Review: Hogendijk, Jan P.; Berggren, J. L. (1989), "Episodes in the Mathematics of Medieval Islam by J. Lennart Berggren", Journal of the American Oriental Society (American Oriental Society) 109 (4): 697–698, doi:10.2307/604119, JSTOR 604119)
- Daffa', Ali Abdullah al- (1977), The Muslim contribution to mathematics, London: Croom Helm, ISBN 0-85664-464-1
- Rashed, Roshdi (2001), The Development of Arabic Mathematics: Between Arithmetic and Algebra, Transl. by A. F. W. Armstrong, Springer, ISBN 0792325656
- Youschkevitch, Adolf P.; Boris A. Rozenfeld (1960), Die Mathematik der Länder des Ostens im Mittelalter, Berlin Sowjetische Beiträge zur Geschichte der Naturwissenschaft pp. 62–160.
- Youschkevitch, Adolf P. (1976), Les mathématiques arabes: VIIIe–XVe siècles, translated by M. Cazenave and K. Jaouiche, Paris: Vrin, ISBN 978-2-7116-0734-1
- Book chapters on Islamic mathematics
- Berggren, J. Lennart (2007), "Mathematics in Medieval Islam", in Victor J. Katz, The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook (Second ed.), Princeton, New Jersey: Princeton University, ISBN 9780691114859
- Cooke, Roger (1997), "Islamic Mathematics", The History of Mathematics: A Brief Course, Wiley-Interscience, ISBN 0471180823
- Books on Islamic science
- Daffa, Ali Abdullah al-; Stroyls, J.J. (1984), Studies in the exact sciences in medieval Islam, New York: Wiley, ISBN 0471903205
- Kennedy, E. S. (1984), Studies in the Islamic Exact Sciences, Syracuse Univ Press, ISBN 0815660677
- Books on the history of mathematics
- Joseph, George Gheverghese (2000), The Crest of the Peacock: Non-European Roots of Mathematics (2nd ed.), Princeton University Press, ISBN 0691006598 (Reviewed: Katz, Victor J.; Joseph, George Gheverghese (1992), "The Crest of the Peacock: Non-European Roots of Mathematics by George Gheverghese Joseph", The College Mathematics Journal (Mathematical Association of America) 23 (1): 82–84, doi:10.2307/2686206, JSTOR 2686206)
- Youschkevitch, Adolf P. (1964), Gesichte der Mathematik im Mittelalter, Leipzig: BG Teubner Verlagsgesellschaft
- Journal articles on Islamic mathematics
- Høyrup, Jens. “The Formation of «Islamic Mathematics»: Sources and Conditions”. Filosofi og Videnskabsteori på Roskilde Universitetscenter. 3. Række: Preprints og Reprints 1987 Nr. 1.
- Bibliographies and biographies
- Brockelmann, Carl. Geschichte der Arabischen Litteratur. 1.–2. Band, 1.–3. Supplementband. Berlin: Emil Fischer, 1898, 1902; Leiden: Brill, 1937, 1938, 1942.
- Sánchez Pérez, José A. (1921), Biografías de Matemáticos Árabes que florecieron en España, Madrid: Estanislao Maestre
- Sezgin, Fuat (1997) (in German), Geschichte Des Arabischen Schrifttums, Brill Academic Publishers, ISBN 9004020071
- Suter, Heinrich (1900), Die Mathematiker und Astronomen der Araber und ihre Werke, Abhandlungen zur Geschichte der Mathematischen Wissenschaften Mit Einschluss Ihrer Anwendungen, X Heft, Leipzig
- Television documentaries
- Marcus du Sautoy (presenter) (2008). "The Genius of the East". The Story of Maths. BBC.
- Jim Al-Khalili (presenter) (2010). Science and Islam. BBC.
External links
- Hogendijk, Jan P. (January 1999). "Bibliography of Mathematics in Medieval Islamic Civilization". http://www.jphogendijk.nl/publ/Islamath.html.
- O'Connor, John J.; Robertson, Edmund F., "Arabic mathematics: forgotten brilliance?", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/HistTopics/Arabic_mathematics.html.
- Richard Covington, Rediscovering Arabic Science, 2007, Saudi Aramco World
|
|||||||||||||||||||||||||||||||||||||||||||